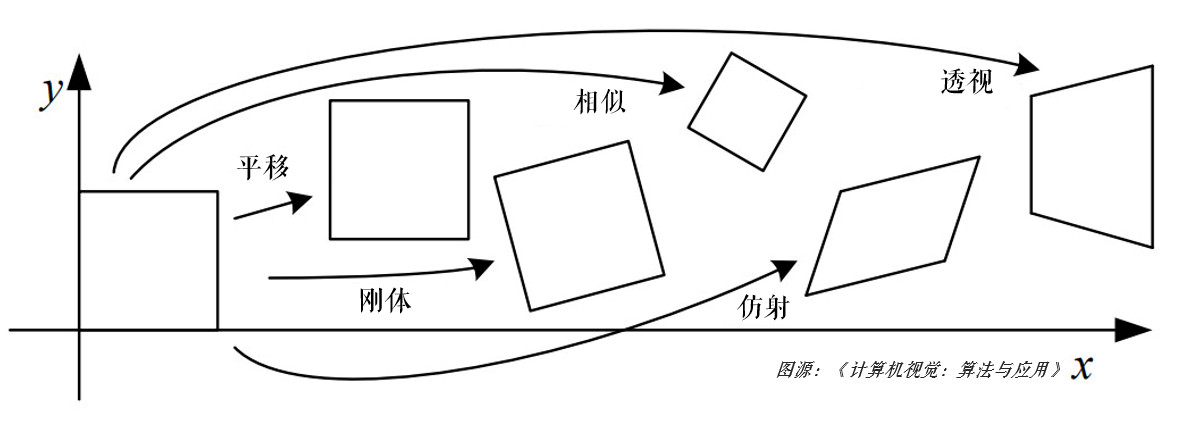
仿射变换与透视变换
仿射变换是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。 基本的图像变换就是二维坐标的变换:从一个二维坐标 $(x, y)$ 到另一个二维坐标 $(u, v)$ 的线性变换: $$ \begin{split} u = a_{1}x+b_{1}y+c_{1} \newline v = a_{2}x+b_{2}y+c_{2} \end{split} $$ 写成矩阵的形式: $$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} \newline a_{2} & b_{2} \end{bmatrix} \begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} c_{1} \newline c_{2} \end{bmatrix}$$ $$R=\begin{bmatrix} a_{1} & b_{1} \newline a_{2} & b_{2} \end{bmatrix},t=\begin{bmatrix} c_{1} \newline c_{2} \end{bmatrix},T=\begin{bmatrix} R & t \end{bmatrix}$$ 矩阵 $T$ 就是仿射变换的变换矩阵,$R$ 为线性变换矩阵,$t$ 为平移矩阵,简单来说,仿射变换就是线性变换+平移。变换后直线依然是直线,平行线依然是平行线,直线间的相对位置关系不变,因此非共线的三个对应点便可确定唯一的一个仿射变换,线性变换 4 个自由度 + 平移 2 个自由度 →仿射变换自由度为 6。 ...