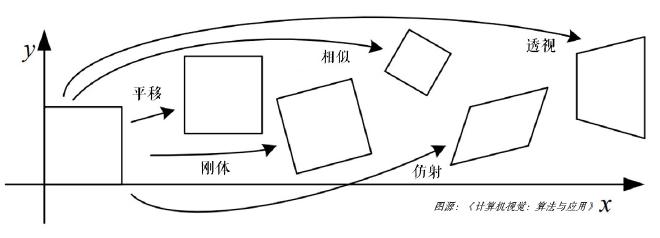
仿射变换#
仿射变换是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
基本的图像变换就是二维坐标的变换:从一个二维坐标 \((x, y)\) 到另一个二维坐标 \((u, v)\) 的线性变换:
$$ \begin{split} u = a_{1}x+b_{1}y+c_{1} \newline v = a_{2}x+b_{2}y+c_{2} \end{split} $$
写成矩阵的形式:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} \newline a_{2} & b_{2} \end{bmatrix} \begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} c_{1} \newline c_{2} \end{bmatrix}$$
$$R=\begin{bmatrix} a_{1} & b_{1} \newline a_{2} & b_{2} \end{bmatrix},t=\begin{bmatrix} c_{1} \newline c_{2} \end{bmatrix},T=\begin{bmatrix} R & t \end{bmatrix}$$
矩阵 \(T\) 就是仿射变换的变换矩阵,\(R\) 为线性变换矩阵,\(t\) 为平移矩阵,简单来说,仿射变换就是线性变换+平移。变换后直线依然是直线,平行线依然是平行线,直线间的相对位置关系不变,因此非共线的三个对应点便可确定唯一的一个仿射变换,线性变换 4 个自由度 + 平移 2 个自由度 →仿射变换自由度为 6。
其实平移、旋转、缩放和翻转等变换就是对应了不同的仿射变换矩阵。
平移#
平移就是 x 和 y 方向上的直接移动,可以上下/左右移动,自由度为 2,变换矩阵可以表示为:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} 1 & 0 \newline 0 & 1 \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} t_{x} \newline t_{y} \end{bmatrix}$$
旋转#
旋转是坐标轴方向饶原点旋转一定的角度 \(\theta\),自由度为 1,不包含平移,如顺时针旋转可以表示为:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \newline \sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} 0 \newline 0 \end{bmatrix}$$
翻转#
翻转是 x 或 y 某个方向或全部方向上取反,自由度为 2,比如这里以垂直翻转为例:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} 1 & 0 \newline 0 & -1 \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} 0 \newline 0 \end{bmatrix}$$
刚体变换#
旋转 + 平移也称刚体变换,就是说如果图像变换前后两点间的距离仍然保持不变,那么这种变化就称为刚体变换。刚体变换包括了平移、旋转和翻转,自由度为 3。变换矩阵可以表示为:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \newline \sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} t_{x} \newline t_{y} \end{bmatrix}$$
由于只是旋转和平移,刚体变换保持了直线间的长度不变,所以也称欧式变换(变化前后保持欧氏距离)。
缩放#
缩放是 x 和 y 方向的尺度(倍数)变换,在有些资料上非等比例的缩放也称为拉伸/挤压,等比例缩放自由度为 1,非等比例缩放自由度为 2,矩阵可以表示为:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} s_{x} & 0 \newline 0 & s_{y} \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} 0 \newline 0 \end{bmatrix}$$
相似变换#
相似变换又称缩放旋转,相似变换包含了旋转、等比例缩放和平移等变换,自由度为 4。在 OpenCV 中,旋转就是用相似变换实现的:若缩放比例为 \(scale\),旋转角度为 \(\theta\),旋转中心是\((center_{x}, center_{y})\),则仿射变换可以表示为:
$$\begin{bmatrix} u \newline v \end{bmatrix} = \begin{bmatrix} \alpha & \beta \newline -\beta & \alpha \end{bmatrix}\begin{bmatrix} x \newline y \end{bmatrix} + \begin{bmatrix} (1 - \alpha ) center_{x} - \beta center_{y} \newline \beta center_{x} + (1 - \alpha ) center_{y} \end{bmatrix}$$
$$\alpha = scale \cdot \cos \theta , \beta = scale \cdot \sin \theta$$
透视变换#
透视变换是将二维的图片投影到一个三维视平面上,然后再转换到二维坐标下,所以也称为投影映射。简单来说就是二维 → 三维 → 二维的一个过程。
$$ \begin{split} X = a_{1}x+b_{1}y+c_{1} \newline Y = a_{2}x+b_{2}y+c_{2} \newline Z = a_{3}x+b_{3}y+c_{3} \end{split} $$
写成矩阵的形式:
$$\begin{bmatrix} X \newline Y \newline Z \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} & c_{1} \newline a_{2} & b_{2} & c_{2} \newline a_{3} & b_{3} & c_{3} \end{bmatrix} \begin{bmatrix} x \newline y \newline 1 \end{bmatrix}$$
其中,\(\begin{bmatrix} a_{1} & b_{1} \newline a_{2} & b_{2} \end{bmatrix}\) 为线性变换,\(\begin{bmatrix} a_{3} & b_{3} \end{bmatrix}\) 为透视变换,\(\begin{bmatrix} c_{1} \newline c_{2} \newline c_{3} \end{bmatrix}\) 为平移变换,因此仿射变换是透视变换的子集。
接下来再通过除以 \(Z\) 轴转换成二维坐标:
$$ \begin{split} x^{’}=\frac{X}{Z}= \frac{a_{1}x+b_{1}y+c_{1}}{a_{3}x+b_{3}y+c_{3}} \newline y^{’}=\frac{Y}{Z}= \frac{a_{2}x+b_{2}y+c_{2}}{a_{3}x+b_{3}y+c_{3}} \end{split} $$
透视变换相比仿射变换更加灵活,变换后会产生一个新的四边形,但不一定是平行四边形,所以需要非共线的四个点才能唯一确定,原图中的直线变换后依然是直线。因为四边形包括了所有的平行四边形,所以透视变换包括了所有的仿射变换。
