A basic 3D rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs.
Left and right hand rule
For left-hand rule, the turn is clockwise, and for right-hand rule, the turn is counter-clockwise.
$$ \begin{split} R_x(\theta) &= \begin{bmatrix} 1 & 0 & 0 \newline 0 & \cos\theta & -\sin\theta \newline 0 & \sin\theta & \cos\theta \end{bmatrix} \newline R_y(\theta) &= \begin{bmatrix} \cos\theta & 0 & \sin\theta \newline 0 & 1 & 0 \newline -\sin\theta & 0 & \cos\theta \end{bmatrix} \newline R_z(\theta) &= \begin{bmatrix} \cos\theta & -\sin\theta & 0 \newline \sin\theta & \cos\theta & 0 \newline 0 & 0 & 1 \end{bmatrix} \end{split} $$
Other 3D rotation matrices can be obtained from these three using matrix multiplication. For example, a rotation whose yaw, pitch and roll angles are \(\alpha\), \(\beta\) and \(\gamma\). It is an intrinsic rotation whose Tait–Bryan angles are \(\alpha\), \(\beta\), \(\gamma\), about axes \(z\), \(y\), \(x\), respectively.
$$ \begin{split} R &= R_z(\alpha)R_y(\beta)R_x(\gamma) \newline &= \begin{bmatrix} \cos\alpha\cos\beta & \cos\alpha\sin\beta\sin\gamma - \sin\alpha\cos\gamma & \cos\alpha\sin\beta\cos\gamma + \sin\alpha\sin\gamma \newline \sin\alpha\cos\beta & \sin\alpha\sin\beta\sin\gamma + \cos\alpha\cos\gamma & \sin\alpha\sin\beta\cos\gamma - \cos\alpha\sin\gamma \newline -\sin\beta & \cos\beta\sin\gamma & \cos\beta\cos\gamma \end{bmatrix} \end{split} $$
Euler angles can be defined by elemental geometry or by composition of rotations. The geometrical definition demonstrates that three consecutive elemental rotations (rotations about the axes of a coordinate system) are always sufficient to reach any target frame.
The three elemental rotations may be extrinsic (rotations about the axes xyz of the original coordinate system, which is assumed to remain motionless), or intrinsic (rotations about the axes of the rotating coordinate system XYZ, solidary with the moving body, which changes its orientation with respect to the extrinsic frame after each elemental rotation).
Without considering the possibility of using two different conventions for the definition of the rotation axes (intrinsic or extrinsic), there exist twelve possible sequences of rotation axes, divided in two groups:
- Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)
- Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)
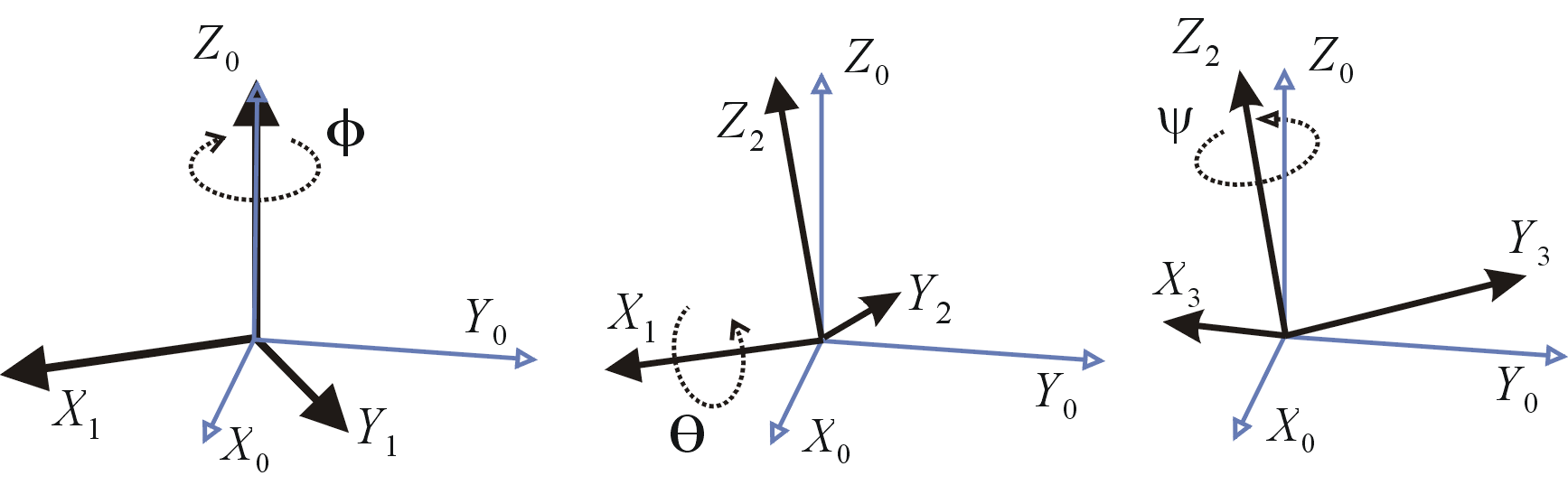
A rotation represented by Euler angles (\(\alpha, \beta, \gamma\)) = (−60°, 30°, 45°), using z-x-z intrinsic rotations.
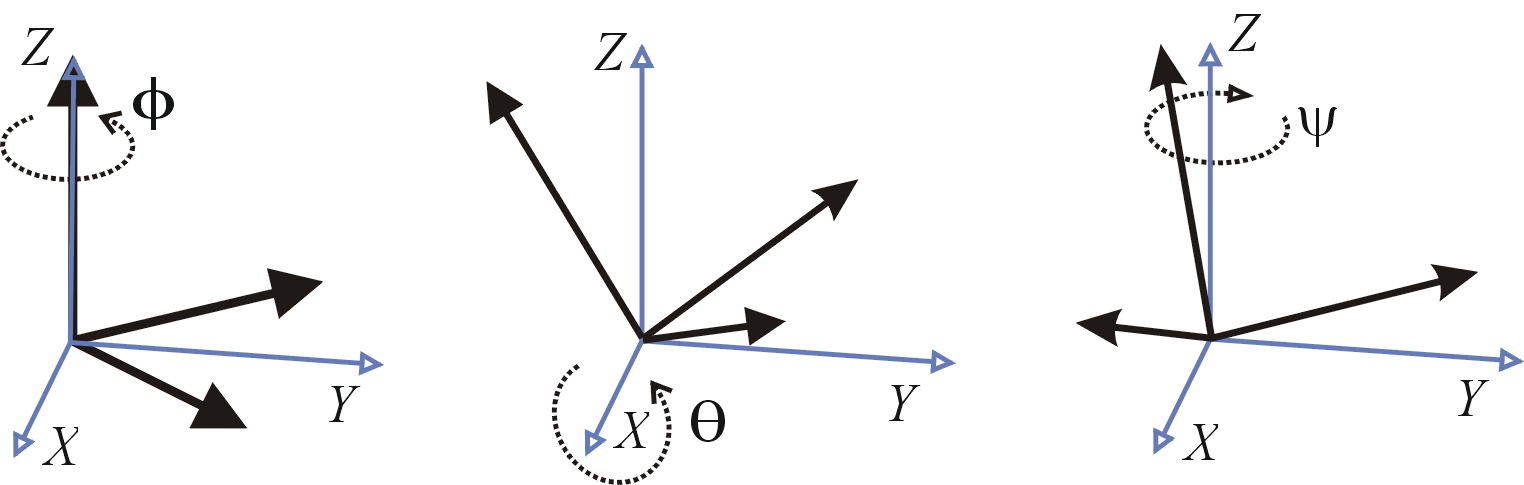
The same rotation represented by (\(\gamma, \beta, \alpha\)) = (45°, 30°, −60°), using z-x-z extrinsic rotations.